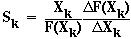- Planning involves identifying the key activities of the project (the tasks) and
ordering them into the proper sequence, while scheduling consists of putting the
plan into the required time frame. Your goal should be to scope the problem so
that you get an answer on time even though it may be necessary to sacrifice
accuracy and sophistication to meet the deadline. The schedule must be
continually updated and the scope and sophistication altered as necessary.
- Following the methodology recommended here and in the following sections, ensures an early solution (approximate), and whatever time remains can be used to improve the accuracy.
- Bear in mind that the design of a complex system is a multi-disciplinary, multi-task effort where one task depends upon the successful completion of other tasks. A proper schedule will include man-power requirements and allow them to be leveled over time so that there is no idle time. There are many scheduling methods available, ranging from simple bar charts to computer-based scheduling systems such as CPM (critical path method) and PERT (program evaluation and review technique). The planning and scheduling of the preliminary design activity, is of course only a part of the planning devoted to the total design/manufacturing.
- Following the methodology recommended here and in the following sections, ensures an early solution (approximate), and whatever time remains can be used to improve the accuracy.
- 3.1 Approach
- Planning
- This constitutes the plan we use to solve the design problem.
Ullman suggests 4 different kinds of plans:- fixed plan: fully specified steps, or "cookbook" approach
- list of plans: select one from a list of solution approaches taken from previous experience
- parameterized plan: a set of steps is prescribed along with the design parameters
- search: a search is made through a number of design solutions.
- list of plans: select one from a list of solution approaches taken from previous experience
Key parts of the approach plan include:- Clear understanding of the problem statement
- Specifying the criteria
- What basic physical principles are involved?
- Word description of steps to be taken
- Lay out tasks involved
- Gathering information
- Specifying the criteria
- Scheduling
- Scheduling of efforts within tasks and to meet the final presentation objective are much the same as discussed under Management above.
- This constitutes the plan we use to solve the design problem.
- 3.2 Modeling
- Physical Model
- Sketch of Device(s)
- Label parts clearly
- Design Criteria
-
The design criterion functions are the objectives in functional form
(dependent variables);
They are the state variables used to make the evaluation of the criterion specified for solution, while satisfying the design requirements
In some cases the criterion function may be obvious, perhaps the total manufactured cost or the life cycle cost of an item; but in other cases it can be difficult to define.
In fact it is sometimes necessary to include more than one criterion. A single composite objective may then be taken as a weighted average of 2 or more individualcriteria. Let us suppose there are n such objective functions and we can write the composite criterion :
The scaling factor is required to make all contribution have the same, or at least consistent, units (we must be careful not to compare apples with oranges). Where possible it is probably better to use a single criterion. Then, if time and need exist, a second one might be assessed to aid in making trade-offs. The importance of choosing and justifying an appropriate objective or composite objective though, cannot be over-stressed. - Mathematical Model
- Functional Constraints
- Use simplest equation/tabular relations which will give sufficiently accurate answers to establish feasibility
- Refine these equations to give the necessary accuracy when proceeding to the Evaluation step
- List those functional constraints which give the defining equations for the Design Criteria (Do not list functions defining inequality constraint variables here)
- List assumptions made and resulting limitations
- fixed by nature
- fixed in problem statement
- fixed by designer
- For the first time through:
- Give a "best guess" value to all state variables
- Use values from a pre-existing, well-understood solution wherever possible i.e. Build upon what you know already.
Justify values given - Use values from a pre-existing, well-understood solution wherever possible i.e. Build upon what you know already.
- Give a "best guess" value to all state variables
- Perform degrees of freedom budget if appropriate
- Develop & list functional expressions for the constrained (inequality) variables
- Design requirements are specified by federal &state regulations, the conceptual designer, the customer, the designer
Fixed Constraints
- List fixed constraints
Design Parameters
- List the design variables.
(These are the state variables which are to be varied to satisfy the Criterion Functions)Inequality Constraints
- 3.3 Nominal Solution
- Analysis
- The initial goal is to obtain a single feasible solution for each concept
and then
be in a position to understand the problem and the importance of each of
the design parameters (some were previously estimated).
(May be able to use simple calculator-based estimates for this purpose and improve the accuracy at a later iteration) - Develop a solution algorithm for the Criteria Functions using the constraint sets developed above
- Note: some of the equations may be transcendental and require using an iterative root-solving routine.
- Develop algorithms for determining inequality constraint functions
- If you are certain your solution must lie on an inequality line, you may find it convenient to change it to a functional constraint. This too, is often transcendental in nature and requires iteration using a root solver.
- Obtain a solution
- The initial goal is to obtain a single feasible solution for each concept
and then
be in a position to understand the problem and the importance of each of
the design parameters (some were previously estimated).
- Feasibility Assessment
- Change design parameters until feasible results (all constraints satisfied) are obtained
- If a physical feasible result cannot be achieved for any concept make certain you understand why, and can defend your conclusion
- Re-assess the problem statement particularly with regard to the fixed constraints imposed.
- If these cannot be altered, discard the non-feasible concepts.
- 3.4 Evaluation & Decision
- There are some dangers in applying this approach to determining which
variables result in the highest sensitivity since, if the nominal solution happens
to be near an optimum solution then S ~ 0. It is necessary to determine S at several
widely dispersed points in the feasible design space therefore.
Comparison of the sensitivities of each design variable will then allow a
determination of which design variables may be given a fixed value, and
thereby reduce the number of degrees of freedom of the problem.
- The carpet/contour plot of course gives us an excellent indication of where these sensitivities should be determined. In fact if the design parameters are all chosen to be non-dimensional the slope of lines on the carpet plot can be used as direct indications of relative sensitivities of the parameters.
- Iteration
Here we begin to march toward a solution which satisfies the criterion. We will assume that this involves a means-end process like an optimization process and we are attempting to minimze a criterion function. If the preceding steps have been followed properly, then the problem is well-posed and there is a unique, best solution which of course satisfies the inequality constraints.
Since in general, some of our equations in engineering design are in tabular and graphical form it is not possible to use some of the mathematical tools, such as Lagrange multipliers, to search for optima. Instead we use numerical-based approaches. There are two general approaches commonly used:- A Graphical Data Base Search
- A graphical display of the design space allows us not only to find the optimum, but also to "see" the solution behavior near the optimum. The disadvantage lies primarily in calculating and storing the huge data bases required, and in our inability to display graphical solutions where there are many degrees of freedom to the problem; it is difficult to plot a surface in multi-dimensional space. In any event, the graphical display should always be used to follow the solution, making sure that it is behaving properly prior to attempting a direct numerical optimization.
It is sometimes possible to reduce the effective number of degrees of freedom by using optimal relations for a few of the design parameters within the algorithm.- A Numerical Search
- The inequality constraints are translated into equations or are treated as boundaries, and a search is made for the appropriate extreme in the criterion function; most available software requires that the criterion function be written in such a fashion that a minimum is to be obtained. There are computer programs available using a variety of approaches, beyond our scope here, which search for the optimum.
- A graphical display of the design space allows us not only to find the optimum, but also to "see" the solution behavior near the optimum. The disadvantage lies primarily in calculating and storing the huge data bases required, and in our inability to display graphical solutions where there are many degrees of freedom to the problem; it is difficult to plot a surface in multi-dimensional space. In any event, the graphical display should always be used to follow the solution, making sure that it is behaving properly prior to attempting a direct numerical optimization.
The disadvantage of this approach is that the end result is a "number"; no indication is given to us of the properties of the solution, such as how broad is the optimum, how sensitive is the answer to a relaxing of inequality constraints unless they are treated as parametric constraints. This is overcome by altering the constraint line and assessing the sensitivity of the criterion function to that change, or by the use of combined graphical/search methods.- The approach to be used is obviously dependent upon the problem complexity. For our purposes we will limit ourselves to the graphical approach for small problems since it is normal to have a graphical display in a workstation environment for fast interaction between designer and computer. For large problems, (those with many degrees of freedom) we will use numerical search techniques after an initial graphical study.
- 4. PRESENTATION
- The carpet/contour plot of course gives us an excellent indication of where these sensitivities should be determined. In fact if the design parameters are all chosen to be non-dimensional the slope of lines on the carpet plot can be used as direct indications of relative sensitivities of the parameters.
Then the sensitivity of the objective function to any design variable can be defined as